개요
연관규칙분석은 두 아이템 집합 (단일 아이템이 아님) 의 발생 규칙을 분석하는 것이다. 가장 쉬운 예로 매점에서 "삼각김밥을 사는 사람은 라면도 같이 구매할 가능성이 높다" 와 같은 규칙을 찾는 것이다.
활용분야는 무궁무진하다. 물론 어떻게 사용하느냐에 따라서이겠지만.. 인터넷 광고에서 자동차 광고를 끝까지 본 사람은 차량 용품 광고에 반응할 것이다 라든지, xx에 취약점이 있는 시스템은 xx에도 취약할 가능성이 높다 와 같이 보안 분야에도 활용할 수 있겠다.
예제
다음 11명의 학생이 좋아하는 스포츠이다. 1이 좋아한다는 것, 0이 아님을 의미한다.
| Name | baseball | basketball | soccer |
|---|---|---|---|
| jacob | 1 | 1 | 0 |
| noah | 1 | 1 | 1 |
| george | 0 | 1 | 1 |
| oscar | 0 | 1 | 1 |
| leo | 0 | 1 | 0 |
| logan | 1 | 1 | 0 |
| theo | 1 | 0 | 0 |
| james | 1 | 0 | 1 |
| joshua | 0 | 0 | 1 |
| henry | 0 | 1 | 0 |
| max | 1 | 0 | 0 |
jacob은 야구와 농구를, noah는 모든 스포츠를 좋아한다 고 해석할 수 있다.
규칙
규칙을 만들기에 앞서 조건절(Antecedent)와 결과절(Consequent)에 대한 개념이 필요하다. 조건절 -> 결과절이라고 보면 된다. 예를 들어 {야구와 농구}를 좋아하는 사람은 {축구}도 좋아한다 에서 {야구와 농구}, {축구}가 아이템 집합이 되고, {야구와 농구}를 좋아함이 조건절, {축구}를 좋아함이 결과절이 된다.
간단한 예제인 11줄의 표에서만 해석해도 상당히 많은 규칙이 경우에 수로 나올 수 있다.
따라서 우리가 관심있는 어떤 규칙이 유의미한 규칙일까? 를 이해하려면 지지도(support)와 신뢰도(confidence), 향상도(lift)를 계산해야 한다.
support(A→B) = P(A)
confidence(A→B) = P(A,B) / P(A)
lift(A→B) = P(A,B) / (P(A) · P(B))
이 세 가지 지표로 규칙들을 비교하여 효과적인 규칙을 찾을 수 있다.
A priori Algorithm
모든 규칙들에 대해 각 지표를 계산한다는 것은 가장 정확한 방법이나 매우 비효율적이다. 연산시간이 기하급수적으로 증가할 것이기 때문이다.
이에 효율적으로 분석할 수 있는 알고리즘이 제안되었는데, 바로 A priori algorithm이다. 핵심 아이디어는 최소한의 지지도(support) 이상만 탐색을 하자는 것이다.
예로 위 예시에서 P({축구})는 약 0.45이다. 축구를 포함한 아이템 집합 즉 예로 P({축구, 농구})는 절대로 P({축구})보다 클 수 없다. {축구}가 {축구, 농구}의 부분집합이기 때문이다. 따라서 최소 지지도를 0.5로 정해버리면 축구가 포함된 조건절에 대해 각 지표들을 계산에서 제외되고 이를 통해 연산 속도를 크게 줄일 수 있다.
R code
sports <- read.csv("H:/home1.csv", header =TRUE, sep=",")
str(sports)
head(sports)
sports_ar<-sports[,-1]
sports_ar$baseball <- as.factor(sports_ar$baseball)
sports_ar$basketball <- as.factor(sports_ar$basketball)
sports_ar$soccer <- as.factor(sports_ar$soccer)
rules <- apriori(sports_ar)
rules <- apriori(sports_ar,parameter = list(supp=0.2, conf=0.2))
inspect(rules)
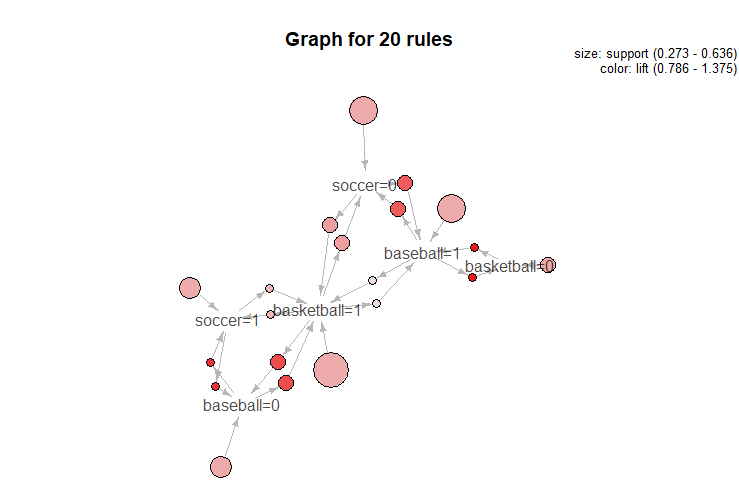
plot(rules, method="graph", control=list(type="items",alpha=1))
apriori 함수가 연관규칙분석하는 함수이고 apriori에 데이터만 넣으면 default 설정으로 동작한다.
다양한 parameter들을 사용할 수 있으니 자세한 사항은 도움말을 참조하면 된다.
결과는 다음과 같은 형태로 나온다.
> inspect(rules)
lhs rhs support confidence lift count
[1] {baseball=0} => {basketball=1} 0.3636364 0.8 1.257143 4
[2] {basketball=0,soccer=0} => {baseball=1} 0.1818182 1.0 1.833333 2
[3] {baseball=0,soccer=0} => {basketball=1} 0.1818182 1.0 1.571429 2