Summary Review
- 대용량의 증거물 (주로 storage media) 에서 특정 파일 혹은 데이터가 존재하는지 효율적으로 찾는 방법을 제안하고자 함, 갈수록 대용량화되고 있는 증거물을 어떻게 효율적으로 조사할 수 있을 지에 대해 영감을 얻을 수 있었음
- 제안하는 기법의 기반이 되는 각종 확률들 / 수치들이 불명확하고 계산이 틀린 것으로 보이는 부분들이 있음. 특히 Region size를 결정하는 합리적인 방안이나 알고리즘에 대한 소개가 없어 활용도는 떨어짐
- 평점 : ★★★☆☆ (한 번쯤 읽어볼만 함)
Detail
Digital Investigation
Volume 24, March 2018, Pages 128-141
https://www.sciencedirect.com/science/article/pii/S1742287617303249
대용량 storage media를 대상으로 특정 파일 혹은 데이터가 존재하는지 효율적으로 검색하기 위해 Random Sampling을 이용하되, 기존의 방법보다 개선된 방법을 제시하는 논문이다.
디지털 포렌식의 challenge로 크게 4가지를 뽑았는데, Increasing Volume of Data, Resource Constraints, Evidence Examination Delay, Heterogeneity of Data 이다. 각각 데이터의 대용량화, 증거 수집 및 보존에 소요되는 Cost (한정되어 있는 예산으로 인한 Constraints), 증거 분석 시간의 증가, 데이터 형태의 다양함을 의미한다.
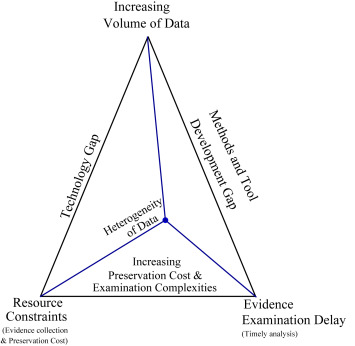
Fig. 1. Proposed digital forensics challenge trade-off.
저자는 조사대상이 되는 Data 자체를 줄이는 것이 효율적인 방법으로 판단했고, 통계적 근거에 의한 Random Sampling이 그 답이라 판단하였다.
Random Sampling의 기본 개념은 쉽게 학창시절 수학시간에 배웠던 항아리에서 파란공을 뽑을 확률 문제를 생각하면 된다.

파란공은 조사자가 찾고자하는 데이터의 sector이고, 그 외의 데이터는 빨간공이라 생각해보자. 그리고 항아리에는 무수히 많은 수에 공들이 들어있어 사람이 모두 확인할 수 없다고 가정하자. 가령 파란공은 4096개, 빨간공은 백만개 정도 들어있다고 생각해보자.
항아리에서 공을 여러개 뽑는다고 했을 때, 파란공을 하나라도 뽑으려면 최소한 몇개의 공 (sample) 을 뽑아야하는 것일까를 고민하는 것이 랜덤 샘플링이라고 이해하면 된다.
저자는 기존에 모든 Sector를 대상으로 Random Sampling을 하는 것은 성능 측면에서 비효율적이므로 Region이라는 가상의 단위를 생성하고 그 안에서 Random Sampling을 하는 방식을 사용하면 프로세스 측면에서도 좋고, 결과물도 Random Sampling과 큰 차이가 없다는 것을 실험을 통해 증명하고자 했다.
In my opinion...
과연 이게 실용성이 있을까? 개인적으로 다음과 같은 문제점들이 있다고 판단된다.
우선 디지털포렌식에서 찾고자하는 정보는 주로 파일 형태로 남아있을텐데 (왜냐면 논문에서 제시한 방법은 어찌 됐든 Input File을 알고 있다는 가정하에 진행되기 때문에) 파일들이 골고루 fragmented 되어 있지 않다면 오히려 강제적으로 Region을 나눈 것이 독이 될 수 있다.
1TB 저장매체에서 2MB의 문서파일을 찾는 논문의 Case study에서 알 수 있듯이 기존 방법에서는 59개의 sector를, 제안하는 방법에서는 37개의 일치하는 sector를 찾았다. 만약 2MB보다 작다면 제안한 방법에서 1개도 못찾았을 가능성도 있으며, 해시가 일치하더라도 오탐이 존재할 수 있기 때문에 좀 더 촘촘한 방법론이 필요하지 않나 생각된다.
두 번째 문제점도 첫 번째와 이어지는 부분인데.. Region 크기에 대한 확률적 기반이 부족하다. 1MB부터 2GB까지 Region에 따른 에러율을 차이를 조사하기도 했는데 읽다보면 so what 이다. case study에서도 512MB를 region으로 사용하는데 그 이유는 딱히 없고 그냥 임의로 정한 듯하다.
디지털 포렌식은 yes or no problem들이 많으므로 확률적 기법을 사용할 땐 그 기반이 탄탄해야 하는데 그런 점에서 아쉬운 논문이긴 하다.
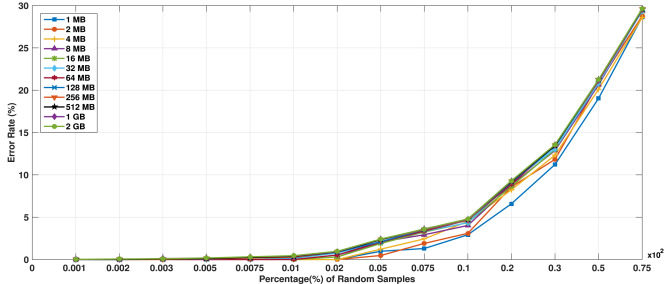
Fig. 12. Analysis of error rate based on the regions of different sizes.