개요
Clustering은 Unsupervised learning 기법에 해당한다.
그말은 즉 데이터들의 정답을 알 수 없다는 말인데... 무슨말인가하면
각 개체의 그룹 정보 없이 비슷한 것끼리 묶는다는 말이다.
예를 들어 아래와 같은 여섯 명의 데이터가 있다고 했을 때,
col2와 col3의 데이터만으로 비슷한 개체끼리 묶는 것을 군집화-Clustering이라 하고
col1, col2, col3 데이터를 이용하여 키와 몸무게로 남/녀를 판단하는 룰을 만드는 것을 분류-Classification이라고 한다.
| gender | height | weight |
|---|---|---|
| 남 | 178cm | 80kg |
| 남 | 182cm | 70kg |
| 남 | 171cm | 75kg |
| 여 | 162cm | 60kg |
| 여 | 170cm | 58kg |
| 여 | 158cm | 48kg |
K-means Clustering은 각 개체간의 거리가 가까운 것끼리 K 개로 군집화하는 것을 의미한다.
각 군집은 하나의 중심을 갖는데, 중심과 가까운 것끼리 모이는 것이다.
식으로 나타내면 다음과 같음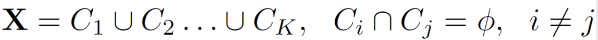
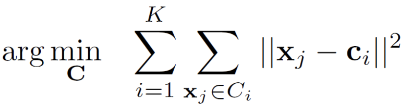
나누어진 군집들의 개체간의 거리를 최소화하는 Cluster 를 찾는게 주 목적으라고 보면 된다. 심플한 원리
R code
Data는 이미 주어져있다고 가정하고
Data_scaled <- scale(Data, center = TRUE, scale = TRUE) # 데이터 정규화
Data_clValid <- clValid(Data_scaled, 2:10, clMethods ="kmeans", validation = "internal",maxitems=nrow(Data_scaled))
summary(Data_clValid )
출력은 다음과 같이 됨
Clustering Methods:
kmeans
Cluster sizes:
2 3 4 5 6 7 8 9 10
Validation Measures:
2 3 4 5 6 7 8 9 10
kmeans Connectivity 81.2151 108.2623 155.4992 187.2956 178.0631 202.9147 288.6968 321.1198 414.0401
Dunn 0.0047 0.0036 0.0042 0.0020 0.0055 0.0060 0.0042 0.0030 0.0025
Silhouette 0.3622 0.5029 0.5467 0.5758 0.5990 0.5438 0.5343 0.5037 0.4607
Optimal Scores:
Score Method Clusters
Connectivity 81.2151 kmeans 2
Dunn 0.0060 kmeans 7
Silhouette 0.5990 kmeans 6
각 index별로 최적의 클러스터를 출력해준다.
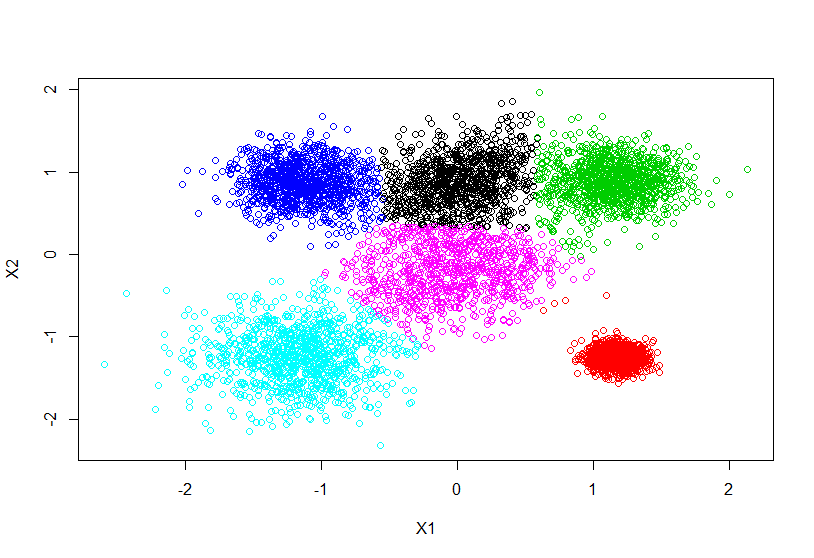
클러스터 수를 6으로 선정했다고 가정하고 K-means 클러스터링을 적용하고 plot을 그리는 코드는 다음과 같다.
Data_kmc <- kmeans(Data_scaled,6)
plot(Data_scaled, col = Data_kmc $cluster)